You won’t see a formula sheet on the ACT Math section, so there are a few math formulas you need to memorize and recall when you take the ACT test.
Often, knowledge of these key formulas can help you solve problems faster and more accurately. Below, you’ll find a list of ACT math formulas to know from every content area in the Math section: Numbers and Quantity, Algebra and Functions, Statistics and Probability, and Geometry.
At the end of the post, you can find a downloadable ACT formula sheet in PDF format.
Important ACT Math Formulas
Number and Quantity
Percents
Calculating percents:
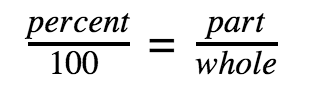
or, change the words to an algebraic equation and solve:
Example: 40% of what is 20?
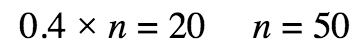
Percent increase or decrease:
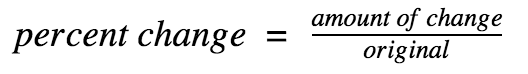
Exponents and Roots
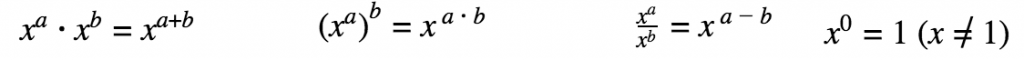
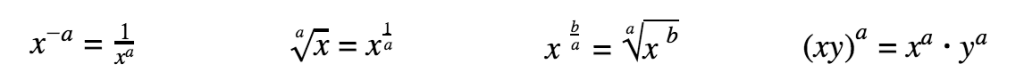
Complex Numbers
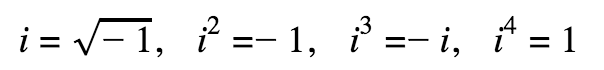
Use the conjugate to eliminate the imaginary:
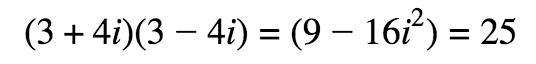
Arithmetic Sequences
Each term (t) is the previous term plus a common difference (d) to find the nth term
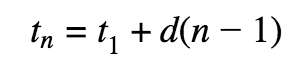
Geometric Sequences
Each term (t) is the previous term times a common ratio (r) to find the nth term
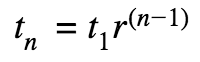
Statistics and Probability
Mean (the average)
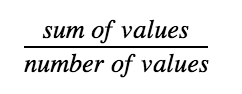
Median
The middle value when items are arranged from least to greatest
Range
The difference between the max value and min value
Mode
The value that occurs the most in a set
Standard Deviation
Shows how spread the data points are.
Low standard deviation:
Data points are closer to the mean
High standard deviation:
Data is spread over a wider range
Probability of an Event
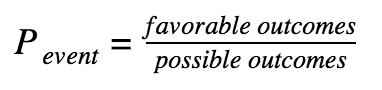
Joint or Conditional Probability
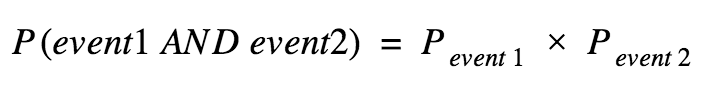
Mutually Exclusive Probability
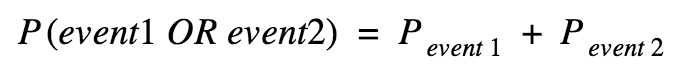
Fundamental Counting Principle
Pick 1 from each group, multiply the number of options in each group
Permutation
A combination of events occurring when order matters and the items cannot be repeated
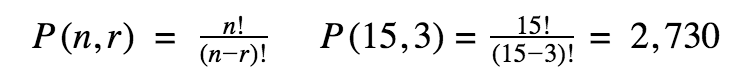
Combination
A combination of events occurring when the order does not matter
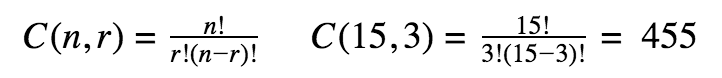
Domain
Set of possible values of x
Range
Set of possible values of y
Algebra and Functions
Lines
The slope of a line:
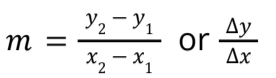
Parallel lines:
Have the same slope
Perpendicular lines:
Have slopes that are negative reciprocals
Slope-Intercept Form
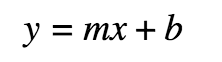
Point-Slope Form
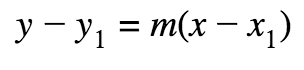
Midpoint Formula
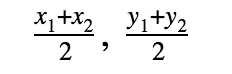
Distance Formula
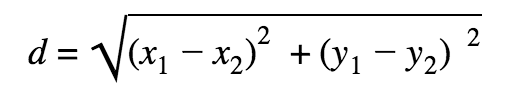
Direct Variation
y=kx where k is the constant of variation
Indirect Variation
yx=k where k is the constant of variation
Standard Form of a Quadratic
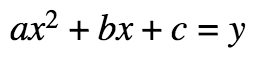
To find the solutions: Set y equal to 0, and solve for x by factoring or use the Quadratic Formula:
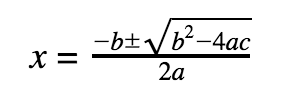
To find the vertex: x = -b/2a, plug value back into the equation to find the y-coordinate
Vertex Form of a Quadratic
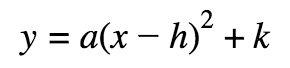
The vertex is (h, k ).
Factored Form of a Quadratic
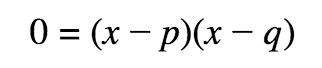
x-intercepts/solutions/zeros are x=p & x=q
Exponential Functions
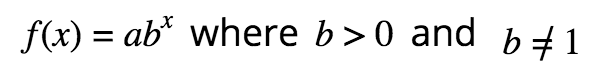
Shows growth if b>1or decay if 0<b<1
Growth/Decay when r is a percent:

Change to decimal, add to 1 if growth, subtract from 1 if decay
Interest compounded n times for t years:

Interest continuously compounded for t years:
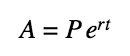
Some Helpful Log Rules

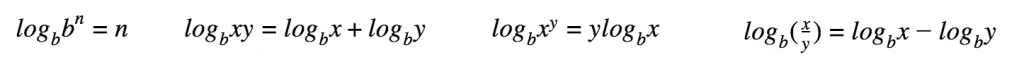
Geometry
Triangles
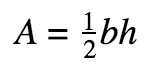
Degrees sum to 180°
Sides
No side can be greater than the sum or less than the difference in length of the other two. Side lengths are in the same ratio as opposite angle measures.
Angles
Complementary angles sum to 90°
Supplementary angles sum to 180°
Exterior angles for ANY polygon sum to 360°.
Interior angles for a polygon sum to 180° (n-2) where n is the number of sides in the polygon.
Special Right Triangles
30, 60, 90 Triangle

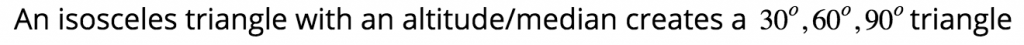
45, 45, 90 Triangle


Rectangular Prism
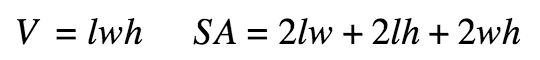
Cylinder
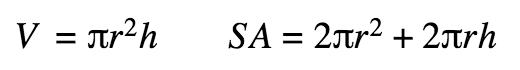
Trigonometric Ratios
Remember these ratios with the acronym “SOH-CAH-TOA”
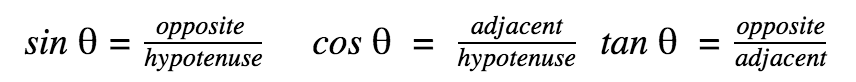
Trigonometric Relationships
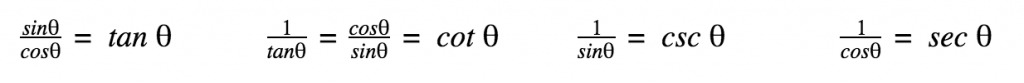
Circles
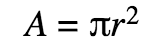

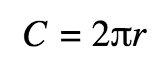
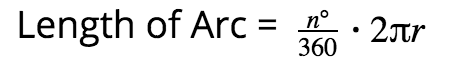
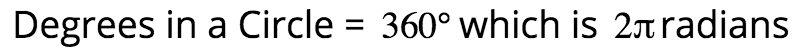

Standard Form of a Circle
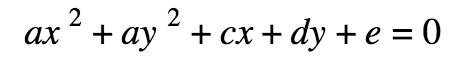
Vertex Form of a Circle
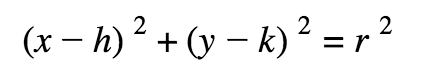
(h, k) is the center and r is the radius
