The SAT provides a reference sheet of math formulas in the SAT math section – but it’s short. You’ll use more formulas on test day than you see on the sheet. The formula list below boils down the formulas you will most likely use on the SAT.
Below, you’ll find a list of SAT math formulas to know from every content area in the Math section: Problem Solving and Data Analysis, Heart of Algebra and Passport to Advanced Math, and Additional Topics in Math.
How to Use These SAT Math Formulas
Maybe you want to print this out for reference, maybe you want to compare these formulas with the very few that are given to you on the SAT, or maybe you want to highlight the formulas you refer to while completing practice problems – then you will know what formulas to study before the test!
Before you get started, a few tips for studying for math:
- Most importantly, work to “own the material.” You will never be able to see every question prior to taking the test, so you need to understand the concepts. That way you can apply your knowledge to novel problems.
- Second, familiarize yourself with the wording of the questions. Practice with questions that are similar to how they will be worded on the actual test. Sometimes standardized test structure is not something with which you are very familiar.
- Then take a timed test. The SAT has free downloadable released tests [LINK]. Make sure you can work under that time crunch. And when you have finished a timed test, find your errors and go back to “owning the material.” Analyze your errors and wrap your brain around the concepts.
Finally, practice does not make perfect. Perfect practice makes perfect!
PS: Download these SAT formulas in PDF format at the end of this post!
The SAT Formula Sheet
These are the formulas given to you in the Math section of your SAT test booklet:
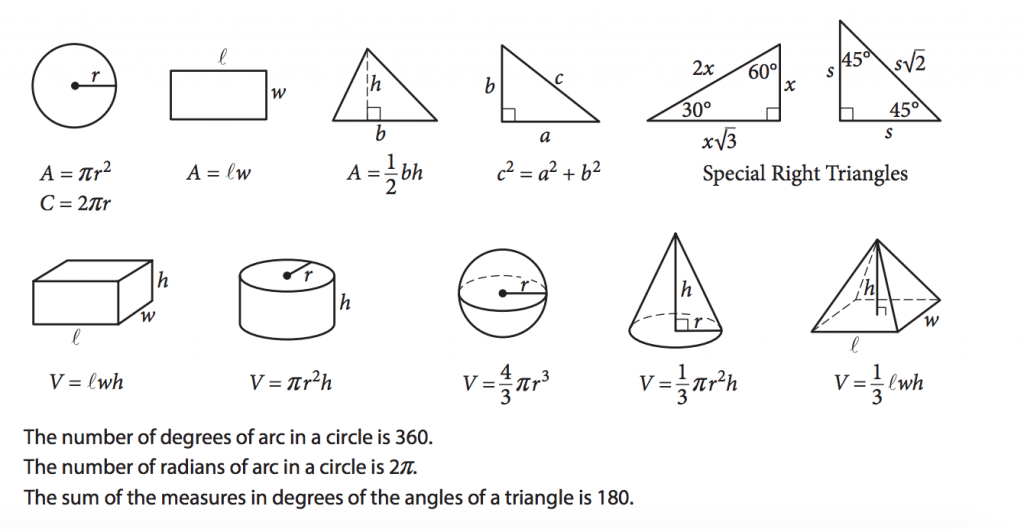
The SAT formula sheet provides basic formulas for circles, area, triangles, and volume. But there many additional formulas it will be helpful to know on test day so you can fly through the math section with confidence.
The Best Calculator to Use on the SAT
Problem Solving and Data Analysis
Percents
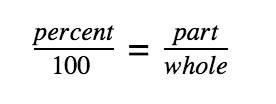
OR change words to an algebraic equation and solve
Example: 40% of what is 20?
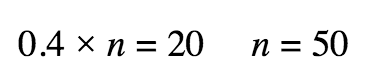
Percent increase or decrease:
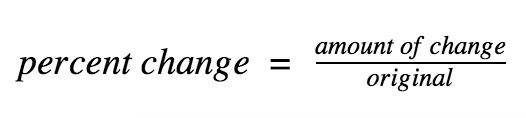
Mean (the average)
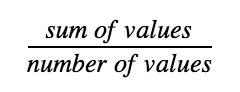
Median
Middle value when items are arranged from least to greatest
Range
The difference between the max value and min value
Mode
Value that occurs the most in a set
Standard Deviation
Shows how spread data points are.
Low standard deviation: data points are closer to the mean
High standard deviation: data is spread over a wider range
Probability of an Event
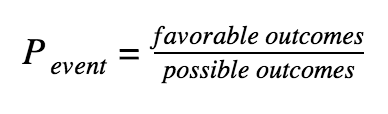
Joint or conditional probability
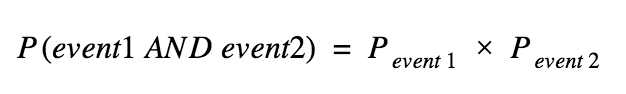
Mutually exclusive probability
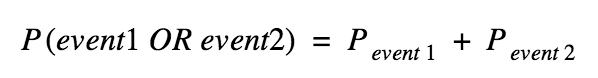
Fundamental Counting Principle
Pick 1 from each group, multiply the number of options in each group
Permutation
A combination of events occurring when order matters and the items cannot be repeated
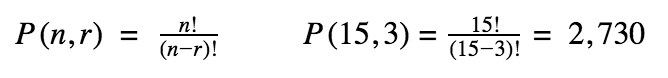
Combination
A combination of events occurring when the order does NOT matter
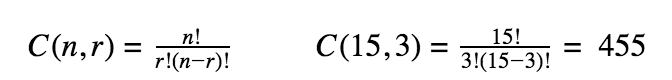
Arithmetic Sequences
Each term (t) is the previous term plus a common difference (d)
to find the nth term:
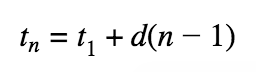
Geometric Sequences
Each term (t) is the previous term times a common ratio (r)
to find the nth term:
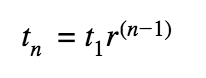
Key Math Section Strategy for the ACT or SAT
Heart of Algebra and Passport to Advanced Math
Domain
Set of possible values of x
Range
Set of possible values of y
Lines
Slope of the line:
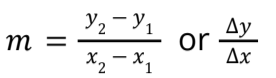
Parallel lines have the same slope and Perpendicular lines have slopes that are negative reciprocals
Slope-intercept form:
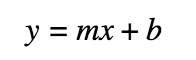
Point-slope form:
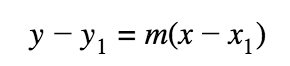
Midpoint Formula
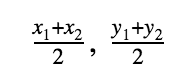
Distance Formula
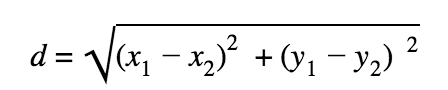
Direct Variation
y=kx where k is the constant of variation
Indirect Variation
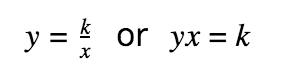
where k is the constant of variation
Standard Form of a Quadratic
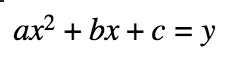
To find the solutions: set y equal to 0, and solve for x by factoring or use the Quadratic Formula
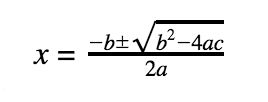
To find the vertex:

plug value back into the equation to find y-coordinate
Vertex Form of a Quadratic
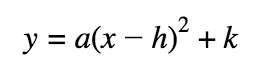
The vertex is (h, k).
Factored Form of a Quadratic
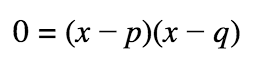
x-intercepts/solutions/zeros are x=p & x=q
Exponential Functions
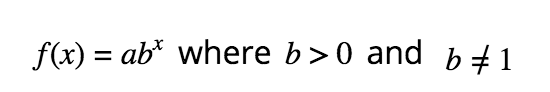
Shows growth if b>1or decay if 0<b<1
Growth/Decay when r is a percent:
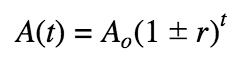

Interest compounded n times for t years:
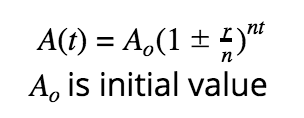
Exponents & Roots
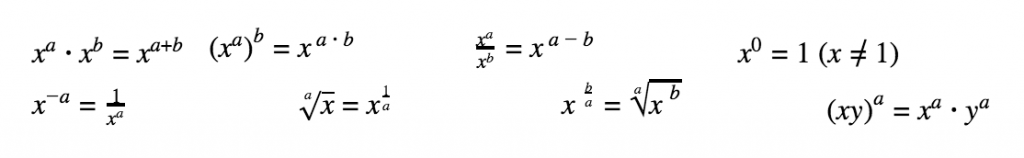
Additional Topics in Math
Complex Numbers
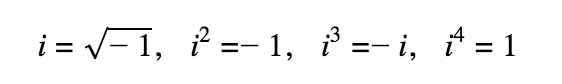
Use the conjugate to eliminate the imaginary:
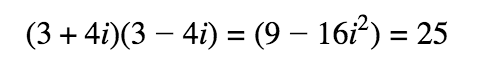
Triangles
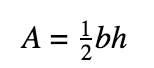
Degrees sum to 180°
Sides: No side can be greater than the sum or less than the difference in length of the other two. Side lengths are in the same ratio as opposite angle measures
Special Right Triangles

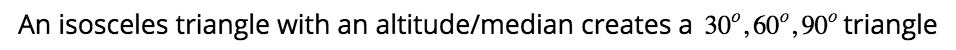


Complementary angles sum to 90°
Supplementary angles sum to 180°
Exterior angles for ANY polygon sum to 360°.
Interior angles for a polygon sum to 180°(n-2) where n is the number of sides in the polygon.
Trigonometric Ratios
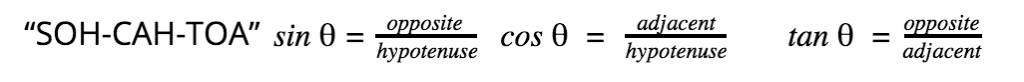
Trigonometric Relationships
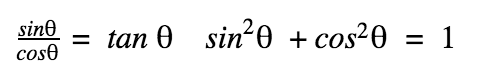
Circle

Degrees in a Circle:
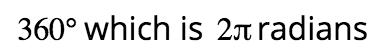
Find radians of given degrees:
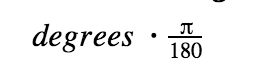
Find degrees of given radians:
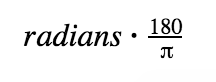
Standard Form of a Circle:
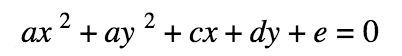
Vertex Form of a Circle:
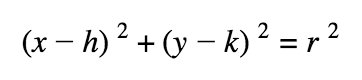
where (h,k) is center and r is radius
Rectangular Prism
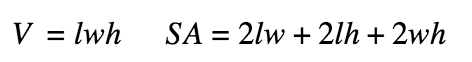
Cylinder
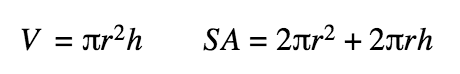

you guys really helped me thank you so much